В типичном классе математики, особенно в средних классах школы, мы склонны использовать одну модель, чтобы связать математику с реальным миром; мы начинаем с обучения математическому содержанию и навыкам, затем мы заставляем учеников практиковаться и выполнять некоторые математические действия, а затем мы можем применить некоторые из этих навыков в контексте реального мира, используя учебные действия, такие как текстовые задачи.

Однако если вы посмотрите на другие модели, например, используемые в международных системах оценки, таких как PISA, вы обнаружите, что моделируется другой процесс.

Ниже представлена ​​схематическая концепция математической грамотности, разработанная для PISA (Международная программа по оценке образовательных достижений учащихся), которая основана на необходимости оценки способности учащихся передавать и применять свои математические знания и навыки для решения задач, возникающих вне контекста школьного обучения. она понятна даже для русскоязычных граждан.

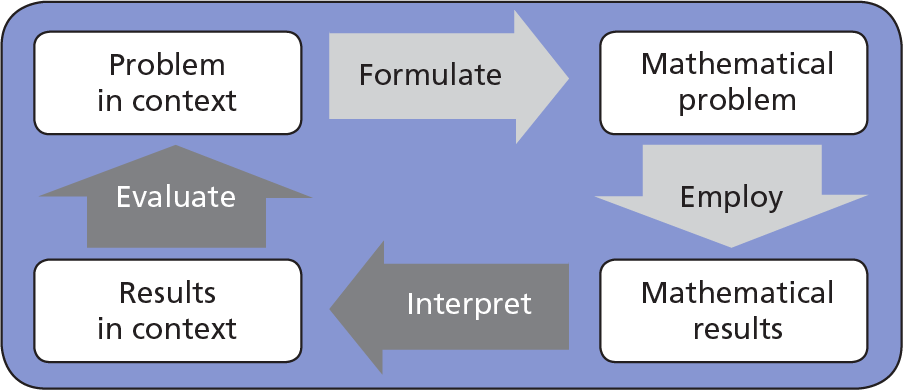
Схематическая концепция математической грамотности, разработанная для PISA.
Оценка и аналитическая основа PISA: математика, чтение, естественные науки, решение проблем и финансовая грамотность. Издательство ОЭСР.

Процессы, описанные в модели, являются ключевыми компонентами решения реальной проблемы, где отправной точкой является проблема в ее контексте, а не математика.

Математическое формулирование ситуаций включает в себя определение того, как применять и использовать математику для решения проблемы, возникающей в реальном мире, — это включает в себя возможность взять ситуацию и преобразовать ее в форму, поддающуюся математическому анализу;

Использование математических понятий, фактов, процедур и рассуждений включает использование математических понятий, процедур, фактов и инструментов для получения математического решения;

Интерпретация и оценка математических результатов включает в себя размышление над математическими решениями или результатами и их интерпретацию или оценку в контексте исходной задачи.

Этот процесс PISA контрастирует с типичной моделью, описанной выше: научите немного математике; попрактиковаться в математике; применить немного математики.

Процесс в реальном мире требует набора различных навыков, выполняемых в обратном порядке — начиная с начальной способности идентифицировать математику в контексте и формулировать ее в виде математической задачи. Затем, второй шаг - сделать математику и применить навыки и знания. Затем учащиеся должны интерпретировать и оценить результаты математических вычислений и подумать о том, как математические результаты применимы и соответствуют реальному миру.

Первая задача в этом цикле PISA — это не то, к чему мы обычно обращаемся на уроках математики, но, возможно, это самая сложная и сложная из всех задач.

В типичном математическом классе основное внимание уделяется первым двум процессам: преподавание математики; попрактиковаться в математике. Если у нас есть время, мы можем часто применять эту математику с помощью текстовых задач, но математические навыки уже определены и сформулированы для ученика (и, как я сказал в разделе «Подключение математики к реальному миру », текстовые задачи часто нереалистичны или не связаны) . к реальным проблемам).

Так что мы можем сделать?

Используйте подход к решению проблем, исследовательский, открытый подход — используйте реальные тексты и реальные ситуации — устанавливайте связи между математикой и реальным миром;

Начните с реального мира — научите учащихся, как выявлять и извлекать математику из запутанных ситуаций реальной жизни, с которыми они, вероятно, столкнутся (то, что я часто называю раскопками математики);

Часть этого состоит в том, чтобы сделать математику явной, а затем, когда возникнет необходимость или появятся пробелы в знаниях, научить математике, которая требуется.
Для вовлеченного и незаинтересованного ученика, а также компетентного и менее компетентного ученика контекст может стать проблемой, мотивацией и целью для понимания и использования математики. Однако для того, чтобы это работало в классе, нам необходимо явно интегрировать описанный выше цикл навыков PISA в преподавание и обучение.